 |
|
For example, the ratio between C and D is 9/8:
These ratios maximize the harmonics in music.
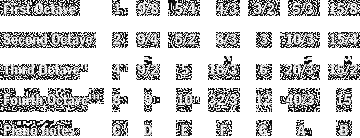
| OCT # | C | C# | D | D# | E | F | F# | G | G# | A | A# | B |
| 1 | 32.703 | 34.648 | 36.708 | 38.891 | 41.203 | 43.654 | 46.249 | 48.999 | 51.913 | 55.000 | 58.270 | 61.735 |
| 2 | 65.406 | 69.296 | 73.416 | 77.782 | 82.407 | 87.307 | 92.499 | 97.999 | 103.83 | 110.00 | 116.54 | 123.47 |
| 3 | 130.81 | 138.59 | 146.83 | 155.56 | 164.81 | 174.61 | 185.00 | 196.00 | 207.65 | 220.00 | 233.08 | 246.94 |
| 4 | 261.63 | 277.18 | 293.66 | 311.13 | 329.63 | 349.23 | 369.99 | 392.00 | 415.30 | 440.00 | 466.16 | 493.88 |
| 5 | 523.25 | 554.37 | 587.33 | 622.25 | 659.26 | 698.46 | 739.99 | 783.99 | 830.61 | 880.00 | 932.33 | 987.77 |
| 6 | 1046.5 | 1108.7 | 1174.7 | 1244.5 | 1318.5 | 1396.9 | 1480.0 | 1568.0 | 1661.2 | 1760.0 | 1864.7 | 1975.5 |
| 7 | 2093.0 | 2217.5 | 2349.3 | 2489.0 | 2637.0 | 2793.8 | 2960.0 | 3136.0 | 3322.4 | 3520.0 | 3729.3 | 3951.1 |
| 8 | 4186.0 | 4434.9 | 4698.6 | 4978.0 | 5274.0 | 5587.7 | 5919.9 | 6271.9 | 6644.9 | 7040.0 | 7458.6 | 7902.1 |
| MIDDLE C IS C4 AT 261.63Hz, CONCERT PITCH IS A4 AT 440Hz. | ||||||||||||
|
Several years ago, astronomer Gerald S. Hawkins, former Chairman of the astronomy department at Boston University, noticed that some of the most visually striking of the crop-circle patterns embodied geometric theorems that express specific numerical relationships among the areas of various circles, triangles, and other shapes making up the patterns (Science News: 2/1/92, p. 76). In one case, for example, an equilateral triangle fitted snugly between an outer and an inner circle. It turns out that the area of the outer circle is precisely four times that of the inner circle. Three other patterns also displayed exact numerical relationships, all of them involving a diatonic ratio, the simple whole-number ratios that determine a scale of musical notes. "These designs demonstrate the remarkable mathematical ability of their creators," Hawkins comments. Hawkins found that he could use the principles of Euclidean geometry to prove four theorems derived from the relationships among the areas depicted in crop circles. He also discovered a fifth, more general theorem, from which he could derive the other four (see recent work, here). "This theorem involves concentric circles which touch the sides of a triangle, and as the [triangle] changes shape, it generates the special crop-circle geometries," he says. Hawkins' fifth crop-circle theorem involves a triangle and various concentric circles touching the triangle's sides and corners. Different triangles give different sets of circles. An equilateral triangle produces one of the observed crop-circle patterns; three isoceles triangles generate the other crop-circle geometries. What is most surprising is that all geometries give diatonic (musical) ratios. Never before (to my knowledge) have geometric theorems been linked with music. Curiously, Hawkins could find no reference to such a theorem in the works of Euclid or in any other book that he consulted. When he challenged readers of Science News and The Mathematics Teacher to come up with his unpublished theorem, given only the four variations, no one reported success. In July 1995, however, "the crop-circle makers . . . showed knowledge of this fifth theorem," Hawkins reports. Among the dozens of circles surreptitiously laid down in the wheat fields of England, one pattern fit Hawkins' theorem based on the stringent definitions, on the rules established by the circles over the period 1980 to the present. NOTE: The circlemakers' fifth theorem has been published in the Mathematics Teacher, the magazine of the National Council of Teachers of Mathematics. Get it through your local library, or order it for US dollars by e-mail Attention "Kay Reuter/Customer Service Dept" orders@nctm.org Ask for information on how to order page 441, volume 91, Number 5. the issue for May, 1998.
|
Equal Tempered Chromatic Music Scale:
Polar Equation: r =261.63*2^(n/12); Note: 261.63 Hertz is the frequency of middle C, and the constant ratio in the sequence is 2^(1/12)=~1.059...Ratio of radius vectors every 360° is ~1.4;Smaller angle between tangent to curve and radius vector is ~ 87.3°PolarPlot[261.63*2^(n/12),{n,0,13}, AspectRatio -> Automatic, PlotStyle->{Thickness[.013],RGBColor[1,0,0]}]; Notice, within each spiral, the growth rate for 360° is a constant and the angle is constant. Each is called an equiangular spiral or logarithmic spiral. Does this relate to astrology? You betcha. |